歡迎光臨德國GMC-I上海電勵(lì)士光伏測(cè)試,專業(yè)光伏組件IV曲線測(cè)試儀生產(chǎn)商 網(wǎng)站地圖 標(biāo)簽索引
歡迎光臨德國GMC-I上海電勵(lì)士光伏測(cè)試,專業(yè)光伏組件IV曲線測(cè)試儀生產(chǎn)商 網(wǎng)站地圖 標(biāo)簽索引
新聞中心ews

全國咨詢熱線13817443004
熱門新聞ot news
聯(lián)系我們ontact

地址:上海市松江漢橋文化科技園B座703

咨詢熱線:13817443004

微信公眾號(hào)
D01:簡(jiǎn)化的雙二極管模型(4個(gè)參數(shù))
為了簡(jiǎn)化PV電池的物理模型,在SDM中,忽略了在p-n結(jié)中由于重組而造成的電流損失。但 是,如果需要更高的精度,則可以并行添加第二個(gè)二極管,以考慮到這一現(xiàn)象,從而獲得DDM(見圖2)。
在這個(gè)模型的D一種方法中,有可能忽略平行阻力Rsh!¥,假設(shè)其為無限值,得到(式( 89)):
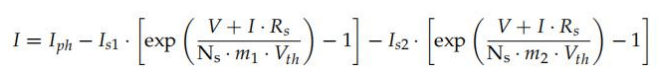
需要識(shí)別的參數(shù)(Iph,是1 , 是2 ,Rs)減少為4,即m1 =1和m2 = 2 . 由于該模型包括D一二 極管的飽和電流和另一二極管的第二飽和電流,為了糾正從初始條件到目標(biāo)條件的I-V曲線, 需要提供兩個(gè)不同的表達(dá)式,允許我們糾正每個(gè)飽和電流,例如(公式(90)和(91)):
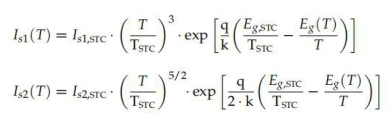
此外,對(duì)于照片生成的電流Iph,再次可以使用(式(76))。Z后,串聯(lián)電阻接收站= 接收站,STC假設(shè)它與G和T無關(guān)。在本文中,我們還提出了被稱為D05的模型,與D01相同, 除了使用(公式(88))而不是(公式(76))。
D02:雙二極管模型(5個(gè)參數(shù))
DDM [57]的完整版本(見圖2)假定平行電阻Rsh的有限值,必須以這種方式(式(14))。對(duì)于串聯(lián)電阻Rs,這個(gè)平行電阻被表示為一個(gè)常數(shù)Rsh= Rsh, STC.必須識(shí)別的參數(shù)將增加到5個(gè):(Iph,STC,是1,STC,是2,STC,接收站,STC,Rsh,STC).被稱為D06的模型是a D02的修改版本,其中使用(式(88))。
D03:雙二極管模型(6個(gè)參數(shù))
為了更好地?cái)M合實(shí)驗(yàn)數(shù)據(jù),文獻(xiàn)[58,91]中的一些作品提出了釋放一個(gè)或兩個(gè)理想性因子。例如,理想性因子m2 第二二極管的范圍在一個(gè)區(qū)間內(nèi),而理想因子是固定的(m1= 1).因此,有一個(gè)額外的參數(shù)需要識(shí)別。同樣,D07是 這種方法,但使用(式(88))進(jìn)行翻譯Iph.
D04:雙二極管模型(7個(gè)參數(shù))
Z后,Z廣義的DDM [20]版本釋放了兩個(gè)理想因子m1 和m2.一方面,這給了模型對(duì)測(cè)量曲 線更好的擬合,但另一方面,也有可能在模型中捕獲高水平的噪聲,導(dǎo)致過擬合[92]。與之前 的模型一樣,本文提出了一個(gè)改進(jìn)的版本D08,以量化在使用(方程(88))時(shí)所取得的改進(jìn)。
羅方法的方法
該方法[59]基于SDM,并試圖從在(G1、T1) . 同樣,目標(biāo)是估計(jì)(Iph1,是1, m,接收站 1,Rsh1).
之后,這些參數(shù)可以轉(zhuǎn)換為其他操作條件,利用這些信息,就可以模擬任何目標(biāo)條件下的 I-V曲線(G2,T2). 然而,與其使用測(cè)量曲線的所有I-V對(duì)作為輸入,不如只考慮來自幾個(gè)選定 點(diǎn)的數(shù)據(jù)。
對(duì)于I-V曲線的每個(gè)工作點(diǎn),包括短路點(diǎn)(SC)、開路點(diǎn)(OC)和Z大功率點(diǎn)(MPP)等, 應(yīng)保持電壓V和(式(9))所述的電壓和電流I之間的關(guān)系。對(duì)于這些點(diǎn)中的每一個(gè),都有可能定 義一個(gè)方程,這樣我們就可以建立一個(gè)系統(tǒng),如果得到與未知數(shù)相同數(shù)量的方程,就可以求解。從SC、OC和MPP中,我們分別有(方程(92)-(94)),它們都是指初始條件(G1,T1):
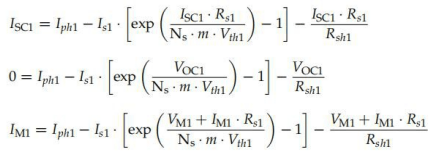
由于我們有五個(gè)未知數(shù),所以需要兩個(gè)額外的方程。一方面, 如果在SC條件下計(jì)算和計(jì)算I對(duì)V的導(dǎo)數(shù),則結(jié)果應(yīng)該是跨越縱坐標(biāo)(V = 0 V)軸時(shí)的I-V曲線 的斜率(公式(95))。這個(gè)斜率dI/dV可以從SC周圍的I-V對(duì)的選擇來估計(jì):

另一方面,當(dāng)穿過橫坐標(biāo)(I = 0 A)軸時(shí),I-V曲線的斜率應(yīng)該等于I對(duì)在OC處計(jì)算的V的 導(dǎo)數(shù),得到Z終的(等式
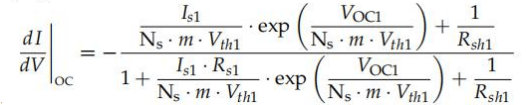
Z后,我們得到了一個(gè)具有五個(gè)未知數(shù)(Iph1,是1, m, 接收站1,Rsh1和五個(gè)方程(式(9 2)-(96))。該系統(tǒng)可以用任何符號(hào)解析器來求解;例如,Matlab [19]的優(yōu)化工具箱。